I recently turned 20; hooray for me! As nice as that would be, unfortunately it would only accurate in base 16.
Sigh. I'm actually 32.
Thirty-two is a power of two (that is, 25 = 32), so it stood out to me given my career in computer science (also the number of bits used to represent integer datatypes I typically have to deal with). It then dawned on me that the next 2n birthday I get to celebrate is, of course, another 32 years away. That's a long time to go; but given the life expectancy for Australian men is just over 80 at the moment, I should be able to see it through. I wonder though, what is the probability of actually surviving the next 32 years?
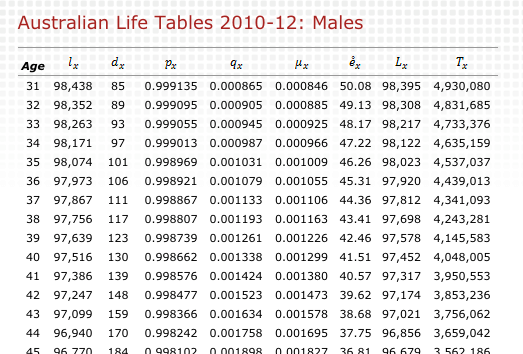
If I understand the life tables properly, and my memory from uni stats classes serves me correctly, multiplying the px values from 32 to 63 should give me the probability of surviving to 64 (since px is the probability of surviving to x+1 years old). That gives me 89.5%. Sounds reasonable, I'll take those odds.
On to something lighter, I did some really in depth research on fascinating facts about the number 32. And by "in depth research", I mean I skimmed the Wikipedia article while commuting to work. Here are the highlights:
- Fifth power of two (25)
- Is a Leyland number; a number that can be written as xy + yx (24 + 42 = 32)
- Is a happy number, yay! (See below)
- 11 + 22 + 33 = 32
- Relating to chess, both black and white have 32 squares of their respective colour on the board; also the total number of pieces on the board. (Also, I suck at chess.)
- Number of teeth in an adult human, including wisdom teeth. I've had three wisdom teeth removed, the fourth doesn't seem to exist (cue jokes about not being so wise)
- As mentioned, number of bits commonly used to represent integer data type
- Number of bits in an IPv4 address
- Twice the number of kilometers I've ever run in a single effort (so far!)
I'm pretty sure happy numbers and Leyland numbers serve no purpose other than recreational mathematics, but like I said, skimming Wikipedia is about as far as I'm willing to go on this subject.
Here's how 32 breaks down as a happy number:
- Start with 32
- 32 + 22 = 9 + 4 = 13
- 12 + 32 = 1 + 9 = 10
- 12 + 02 = 1 + 0 = 1
- 1 (happy!)
So that was a bit of useless fun :-)
